
Closure and its role in the operator hierarchy
Closure indicates the situation in which a group of elements interacts to form a circular pattern. Right at the moment that the interaction cycle closes, and closure has become a fact, the newly formed system attains new properties (also called emergent properties, because they have just emerged) and a higher complexity. Recently, closure obtains much attention in the literature as the most important mechanism for distinguishing systems and creating/recognizing hierarchy (Heylighen 1990, Chandler et al. 2000, Pelster and Kleinert 2002).
Closure plays a major role in the operator hierarchy. The operator hierarchy includes only transitions in which any closure follows immediately after the last preceding, a situation that I named first-next possible closure. First-next possible closure can be used to create a long, unbroken sequence of closures. On the one hand, all the systems in the latter sequence differ from each other because each one of them has a unique number of closures that was required for its formation. On the other hand, the systems can be grouped on the basis of common closure types. These common types are the main organizing principle of the operator hierarchy.
The above presents a short overview of the role of closure in the operator hierarchy. The different aspects of closure and the implications for the operator hierarchy are explained in more detail in the following paragraphs.
1. Introduction to closure. In principle closure is an easy concept. I discuss some examples that show different situations in which closure occurs.
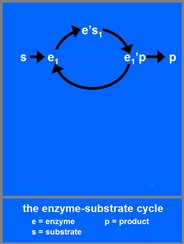
Closure (first order). If schoolchildren give each other a hand and form a large circle, this is an example of closure. Another example is feedback in cybernetic processes where the way in which a system B is affected by a system A depends on the state of system B. An enzyme reaction is a good example of a closed reaction cycle. The cycle starts with the enzyme and a substrate, which together form an enzyme-substrate complex, which changes to an enzyme-product complex, after which the cycle is closed by the splitting up of the complex and the release of the product and the enzyme (see the below graph). Because processes like these involve only a single reaction cycle, they are considered first order closures.
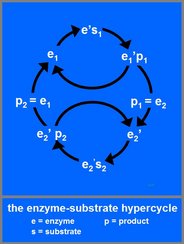
Second order closure. With the above example of the enzyme reaction in mind it is now easy to imagine a situation in which two first order reaction cycles are linked, creating a second order reaction cycle. If we imagine a situation in which the enzyme reaction of the first cycle produces the enzyme that catalyses the second cycle, and the enzyme reaction of the second cycle produces the enzyme that catalyses the first cycle, the result looks like the graph shown here:
A situation like this represents a second order closure or a cycle of cycles and is also regarded as a hypercycle. Different types of hypercyclic closure form the fundaments of the operator hierarchy.
2. Structural and functional closure. The following examples explain the difference between structural closure and functional closure.
Structural closure. Structural closure refers to situation with an explicit spatial character. A structural closure creates a physical limit to one or more properties of a system. The question of what exactly can be called a physical limit depends on the complexity level that is investigated. At the level of the atom, the encapsulation of the nucleus by one or more orbiting electron(s) creates a negatively charged force field around the nucleus. This acts as a spatial ‘shell’ that inhibits free interactions of the nucleus with the surrounding world. At higher levels, structural closure may be more ‘physical’; an example of which is the mediation of autocatalysis by the cell membrane. Structural closure differs from functional closure, where the emphasis is on mutually dependent transformation processes instead of on spatial limits.
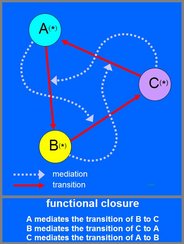
Functional closure. Functional closure can be illustrated by the following example. Let us imagine a small system that consists of three elements A, B and C. Each of these elements can transform one of the others. The element A transforms B to C* (the * indicating that the newly formed element is identical to C but, because it is not C, it is called C*). The element B transforms C to A*. The element C transforms A to B*. As is shown in the below figure, the result of the three processes is that elements A, B and C are transformed to B*, C* and A*. The newly formed A*, B* and C* have the same properties as the former A, B and C. Thus, even though all elements have changed, the result is identical to the original system. All the transformations together have caused no overall change. It is said that the system shows invariance for the sum of all transformations (Heylighen 1989, 1990, 1991).
One kind of functional closure plays a special role in the operator hierarchy. This is the second order functional closure of the hypercycle. A well-known example of a hypercycle is the autocatalytic set. This is responsible for the functioning of the cell (but not for the spatial limits). Every enzyme in the autocatalytic set is involved in a first order cycle of system states. The cycle starts with the binding of the enzyme to a substrate, continues with the formation of a product, and ends with the release of the product en the recreation of the enzyme’s original state, which closes the cycle. If two enzyme cycles exist, based on the enzymes A and B, in which A catalyses the production of B and B catalyses the production of A, a second order cyclic process emerges that reproduces every enzyme involved (and is said to perform autocatalysis). The second order reaction cycle of enzymes has been given the name of hypercycle by Eigen and Schuster (1977) who also explored the dynamic consequences of this type of closure. Additional discussions of hypercyclicity can also be found in Kauffman (1993). Structural and functional closure may occur separately or in combination. Examples of separate occurrence have been discussed above in the form of the cell membrane and the autocatalytic set, respectively. An example of the simultaneous occurrence of structural and functional closure is the integration of (minimally) two cells during the creation of a multicellular organism. The multicellularity of this organism implies a mutual bonding of the cells and thus a structural closure, which is accompanied by a physiological interdependence representing a functional closure. Please notice that without the physiological interdependence, the linked cells form a colony, not an organism (this aspect is discussed in more detail when I discuss the definition of multicellular life). Which aspects are involved in a specific closure depends on the type of closure and the complexity level of the systems involved in the process.
Above, some important aspects of closure have been explained. It has become time to see what closure can do for the analysis of hierarchy. I therefore proceed with discussing how sequential closure steps of the first-next possible closure type can be used to create a strict system hierarchy.
3. First-next possible closure. First-next possible closure is fundamental to the operator hierarchy. It occurs when a first closure that created a system-type A is followed immediately by a second closure that integrates the A type systems into a new system-type B, with exactly one closure existing between the two types. Under the restriction of first-next possible closure any ‘closure-in-between’ has become impossible (by definition).
The name first-next possible closure implies a bottom up (constructivistic/holistic) viewpoint in which a closure event integrates a number of elements into a new, more complex system. For example: interactions between atoms create molecules, cells can interact to become a multicellular life form, etc. A sequence of first-next closures shows how nature produces complexity. There is no problem with turning the reasoning around and basing analyses on the last-preceding possible closure. Last-preceding possible closure can be used for a top down (reductionistic) analysis of how larger systems are composed of small elements. In this way we descend via last-preceding closures into the internal organization of a given system. For example: in a multicellular life form, we find cells, in which we find molecules that are composed of atoms, etc. Note that the use of last-preceding closure excludes organs in multicellulars as well as organelles in cells from the hierarchy, because these elements are the result of internal differentiation after the creation of multicellularity and the cell.
The essence of first-next or last-preceding closure is that both definitions exclude the possibility of closure steps in between of the two levels involved. If ever an additional closure level can be shown to exist, the first-next or last-preceding closure involved has been a misinterpretation that should be improved. From head to tail, the operator hierarchy is based on first-next possible closures. The fact that it should not be possible to insert an additional closure anywhere in the operator hierarchy makes the hierarchy a refutable construction.
I like to stress that first-next closure does not rule out the possibility of the pathways diverging. If two ways of reaching first-next closure exist that are based on the same parental system type, but are based on different principles for reaching closure, they can both become part of the operator hierarchy. An example of this situation is the following: starting with a prokaryotic cell, there exist two possibilities for first-next closure: (1) the creation of prokaryotic multicellularity and (2) the creation of eukaryotic cells.
By using first-next closure a long sequence of hierarchically related system types can be produced. In itself this is not an important achievement. If the periodical system of the elements had ranked atoms simply in a long row according to their individual atomary weight, I would never have become a famous classification. The same applies to the operator hierarchy. It is not sufficient to rank system types simply in a long sequence according to first-next closure. For a more useful classification it is necessary to reveal some kind of underlying logic. In search for such logic I studied the possibilities for classifying the systems in the operator hierarchy according to similar closure types.
4. Groups of systems showing the same closure type. First-next possible closure is a general concept. In the operator hierarchy it has been applied to recognize a long sequence of system types. This includes: the super strings, the quark plasma’s, the hadrons, the atoms, the molecules, the bacterial cells, the eukaryotic cells, the bacterial and eukaryotic multicellulars and the organisms with neural networks (memons).
The above examples show that first-next possible closure covers a broad range of situations that not only show differences in closure patterns, but also similarities. Would it be possible to restructure the above sequence and create a more condensed scheme by grouping systems with similar closure types?
Searching for an answer to the above question, I realized that the interface-closure could act as a border stone in the grouping process. The reason is that the next closure after the interface always belongs to a completely new type, hereby indicating a new group of systems. Because this way of analyzing system complexity was new, I could not use examples from the literature to name the types of closures I recognized and had to introduce new names.
Following the interface closure of the superstrings, a new closure type emerges in quark-gluon plasmas. As this closure involves a second order functional closure, I named it hypercyclicity (after the hypercycle in autocatalytic sets).
Following the closure of the quark confinement, a new closure type emerges in hadrons. As it implies the connecting of similar type units, I gave it the name of multi-stage.
Following the closure of the electron shell, a new closure type emerges in atoms. As it involved the mediating of a hypercyclic system by an interface I named it hypercycle mediating interface (HMI).
Following the closure of the cell membrane, a new closure type emerges in bacteria. As the systems in this state are capable of autonomously copying their information in a structural way (by copying their autocatalytic set, especially their genes), I named it structural copying of information (SCI).
Following the closure of the neural interface, a new closure type emerges in neural network organisms (which I named memons, to distinguish them from gene based organisms). As the systems in this state are capable of autonomous adjustment and even autonomous diversification and selection of their internal neural representations by means of thinking, I named it structural auto-evolution (SAE).
These closures are mentioned here shortly, to explain the choices I made for their naming. I discuss the properties of these operator types in detail in the section ‘closure: types and hierarchical levels’.
5. Closure: A new paradigm for evolution. Armed with the above insights, I created the operator hierarchy. I was surprised to find that limitations in closure configurations apparently have acted as a strong mould for the evolution of system types. Only system types have evolved that fit to this mould. A stunning consequence is that at the level of operators, evolution is not a randomly diverging process. Instead, and in contradiction with common belief, limitations in closure configurations force the evolution of system types to become a deterministic process that can be described by the following logic: In the evolution of system types, every first-next closure either creates a new closure type or repeats an existing one.